Understanding Quick Sort for coding interviews
In the last three posts we looked at selection, bubble and insertion sort respectively. While it’s critical to know these basic sorting techniques, it’s unlikely you’d be asked to code one of these up for your next Microsoft/Google interview unless you’re interviewing for an internship position.
On the contrary, you can expect to be asked to implement quick sort or given a problem that uses a quick sort like technique. Some examples are the Dutch National Flag problem or sorting an array of binary numbers in linear [ O(n)] time.
Strategy for Quick Sort
We’ll use a two phased approach to implement quick sort.
- Phase 1: Partition an array around a pivot element such that all elements smaller than the pivot are to the left of the pivot and all elements bigger than the pivot are to the right of the pivot.
- Phase 2: Recursively divide the array into two parts – to the left of the pivot and to the right of the pivot – and sort each each.
We’ll look at each of the phases in detail with visualizations below.
Phase 1: Algorithm to partition an array
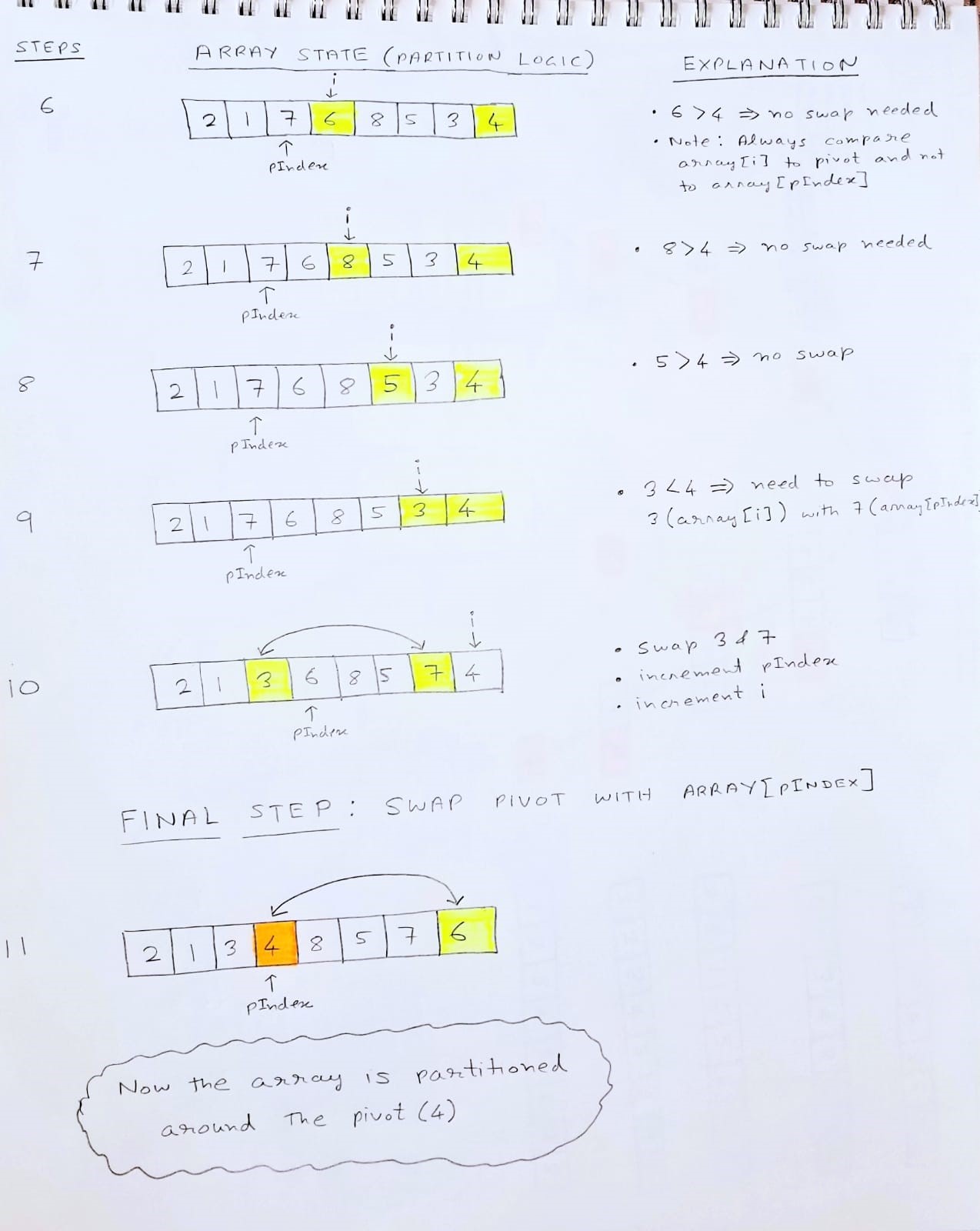
Let’s try to partition the unsorted array below:
7 2 1 6 8 5 3 4
- Select the rightmost element as the pivot ( this could very well have been another element).
- Set pIndex( partition index) to the start of the list.
- Run a loop from i = 0 -> (n-1) and compare each element with the pivot.
- if array[i] < pivot, then swap array[i] with array[pIndex]
- Increment the pIndex
The above steps effectively ensures that all elements lesser than the pivot are pushed to the left of the partition index
- Finally, we swap array[pIndex] with the pivot
Here’s the complete pseudocode for partitioning the array around a selected pivot
Partition( Array, start, end)
{
pivot = Array[end]
pIndex = start
for i = start to (end - 1)
{
if(Array[i] <= pivot))
{
Swap(Array[i], Array[pIndex])
pIndex = pIndex + 1
}
}
Swap(Array[pIndex], pivot)
return pIndex
}Phase 1: Visualize Array partitioning
This is the most important step in this article. I’d highly recommend that you do this yourself on paper or on a whiteboard till you can get the final order correct.
Quick Sort Partitioning Logic Part 1
Quick Sort Partitioning Logic Part 2
Note that:
- The pivot eventually ends up at the final partition index
- All elements smaller than the pivot are to the left of the pivot and all elements larger than the pivot are to the right of the pivot.
- The elements to the left and right of the pivot are not in sorted order among themselves.
Phase 2: Algorithm for Quick Sort
All the heavy lifting is done in phase 1 by the partition function. The algorithm for quick sort goes like this:
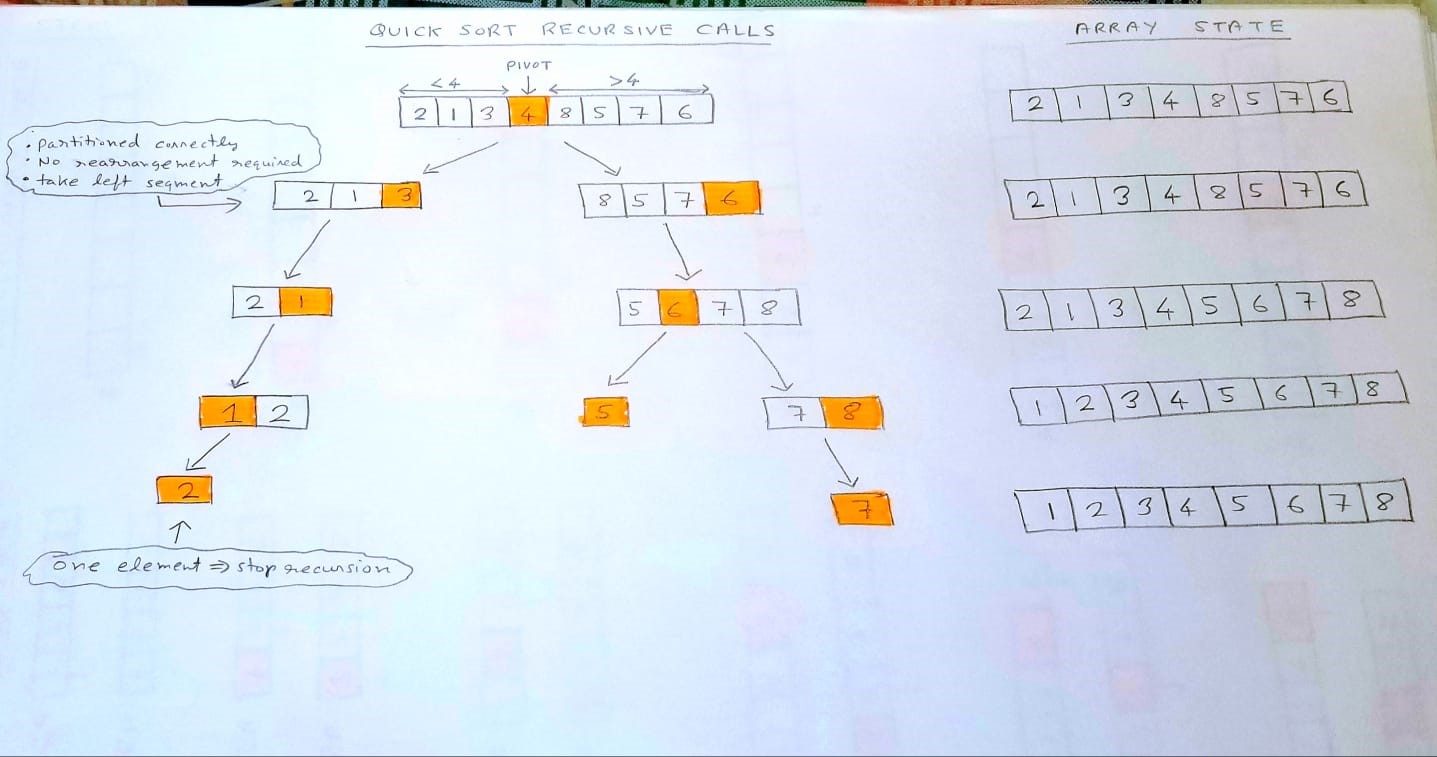
- Given the unsorted array below, select a pivot [Insert picture]
- Rearrange the array such that all elements lesser than the pivot are to the left of the pivot and all elements greater than the pivot are to the right of the pivot. [ picture]
- Once we’ve partitioned the array like this, we can break the problem into two similar sub-problems using a Divide and Conquer strategy. Yes, you’ve guessed it right – the two sub-problems are sorting the segment of the array to the left of the pivot and sorting the segment of the array to the right of the pivot.
Note that unlike Merge Sort, we can do this in place. We just need to keep track of the start and the end index of each segment that we can process recursively.
Here’s the algorithm for quick sort in pseudo code:
QuickSort( Array, start, end)
{
if(start < end)
{
pIndex = Partition( Array, start, end)
QuickSort( Array, start, pIndex - 1)
QuickSort( Array, pIndex + 1, end)
}
}Phase 2: Visualize Quick Sort
The recursive steps are shown below. As always, practice this yourself to fully grok it.
Visualizing Quick Sort
Implementing Quick Sort in C#
using System;
namespace Sorting
{
partial class Sorting
{
// Average case running time = O(nlogn)
// Worst case running time = O(n^2)
// Space Complexity = O(log n) i.e. in place
public static void QuickSort(int[] inputArr)
{
QuickSort(inputArr, 0, inputArr.Length - 1);
}
public static void QuickSort(int[] inputArr, int start, int end)
{
if (start < end)
{
// Partition the array into two parts around the pivot
int partitionIndex = PartitionArray(inputArr, start, end);
//Call QuickSort of the left and right partition
QuickSort(inputArr, start, partitionIndex - 1);
QuickSort(inputArr, partitionIndex + 1, end);
}
}
// Code to partition an array and return the pivot around
// which the array is partitioned
// inputArr: Array which needs to be partitioned
// start: Start index of the array
// end: end index of the array
public static int PartitionArray(int[] inputArr, int start, int end)
{
int pivot = inputArr[end];
int pivotIndex = start;
for (int i = start; i < end; i++)
{
if (inputArr[i] <= pivot)
{
Utilities.Swap(inputArr, i, pivotIndex);
pivotIndex = pivotIndex + 1;
}
}
//Now swap the pivot with element at pivotIndex
Utilities.Swap(inputArr, pivotIndex, end);
return pivotIndex;
}
}
}
Implementing Quick Sort in Java
class Solution
{
public int[] sortArray(int[] nums)
{
quickSort(nums, 0, nums.length-1);
return nums;
}
public static void quickSort(int[] nums, int start, int end)
{
if(start < end)
{
int partitionIndex = partition(nums, start, end);
quickSort(nums, start, partitionIndex-1);
quickSort(nums, partitionIndex+1, end);
}
}
//Randomized partition selection
public static int partition(int[] nums, int start, int end)
{
Random rand = new Random();
int pivotIdx = start + rand.nextInt(end-start + 1);
swap(nums, pivotIdx, end);
int pivot = nums[end];
int pI = start;
int i= start;
while(i < end)
{
if(nums[i] < pivot)
{
swap(nums, i, pI);
pI++;
i++;
}
else
{
i++;
}
}
swap(nums, pI, end);
return pI;
}
private static void swap(int[] nums, int i, int j)
{
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}Note: In the above code snippet, we used random pivot selection as for quick sort as opposed to fixed pivot selection. Let’s explore how this might be helpful in the next section.
Why use random pivot selection in QuickSort ?
In quicksort, the choice of pivot element plays a crucial role in determining the efficiency of the algorithm. QuickSort is a divide-and-conquer sorting algorithm that works by selecting a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays according to whether they are less than or greater than the pivot.
When it comes to pivot selection, using a random pivot is often considered better than deterministic approaches, such as always choosing the first or last element as the pivot. The main advantage of random pivot selection is that it helps to avoid worst-case scenarios and improves the average-case performance of the algorithm.
Here are a few reasons why random pivot selection is beneficial:
- Avoiding Presorted Data Pitfalls: If the input array is nearly sorted or contains repeated elements, always choosing the first or last element as the pivot can lead to worst-case behavior, making the algorithm perform poorly. Random pivot selection helps mitigate this issue by introducing randomness into the choice of pivot, reducing the likelihood of encountering worst-case scenarios.
- Balancing the Partitioning: Randomly choosing a pivot tends to distribute the data more evenly across the partitions. This helps in achieving a more balanced partitioning of the array, which is crucial for the divide-and-conquer strategy to be effective. In contrast, a deterministic choice of pivot might lead to imbalanced partitions, resulting in suboptimal performance.
- Security Against Adversarial Inputs: Using a fixed strategy for pivot selection makes the algorithm susceptible to adversarial inputs that exploit the predictable behavior. Random pivot selection adds an element of unpredictability, making it harder for potential adversaries to craft inputs that would lead to worst-case scenarios.
It’s important to note that while random pivot selection improves the average-case performance of quicksort, it does not eliminate the possibility of worst-case scenarios entirely. However, the average-case time complexity of quicksort with random pivot selection is often very good, making it a practical choice for sorting in many real-world scenarios.
Analysis of Quick Sort
| Sort Property | Analysis |
|---|---|
| Time Complexity | Worst case: O(N^2)Best Case: O(N log N) Average Case: O( N log N) Note: The mathematics involvolving the computation of these is quite involved and rarely show up in interviews. |
| Space Complexity | The in-place partition logic uses O(1) space and the recursive quick sort algorithm takes O(log N) space. So the overall space complexity of quick sort if O(log N) |
| Adaptable | Quick sort is not adaptive |
| Stable | Quick sort is not a stable sort |
When to use and when to avoid Quick Sort ?
Use quick sort in the following scenarios:
- When fast sorting is desired since quicksort has an average case complexity of O(N log N) which is better than bubble or insertion sort.
Avoid using quick sort when:
- When space is limited like in embedded systems
- When ordering of elements matter in the final sorted list , i.e., stable sorting is desired